深度学习(1)：Logistic回归
发表更新学习笔记30 分钟读完 (大约4517个字)0次访问

深度学习(1)：Logistic回归

深度学习（deep learning）是机器学习的一大分支，它试图在机器上建立模仿人脑机制进行分析学习的神经网络，赋予机器解释图像、声音、文本等数据的能力。

这里，首先介绍深度学习中的最基础的学习算法–Logistic回归。

二分类

Logistic回归常用于解决二分类（Binary Classification）问题。在二分分类问题中，对于某个输入，输出的结果是离散的值。

例如：想要构建一个猫图分类器，即输入一张图片，希望该分类器准确判断出该图片是否是一张猫图，并输出它的预测结果。

猫图

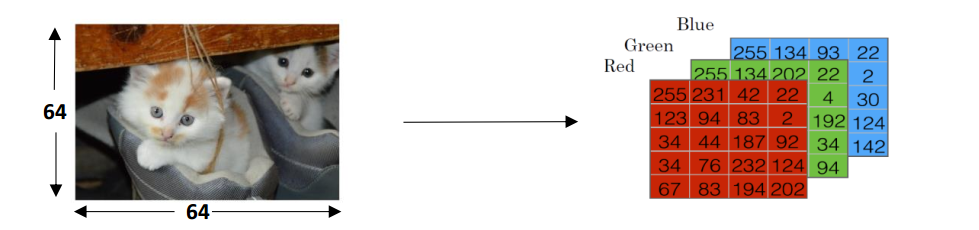
首先，考虑这个猫图分类器的输入。图片是一类非结构化的数据，一张图片在计算机中以RGB编码时，是以红、绿、蓝为三基色，每个像素点上三基色对应的量的多少（即“亮度”）编码为数据进行存储。那么在计算机上，一张图片就可以由大小与图片一致的三个矩阵来表示，三个矩阵分别表示各颜色通道，矩阵中的值则表示各像素值。由此，上图中的猫图大小为$64 \times 64$，便可以表示为三个大小为$64\times64$的矩阵。

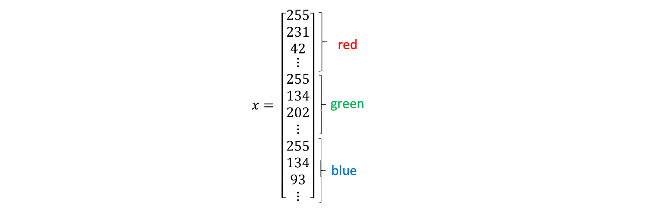
然而，在模式识别（Pattern Recognition）以及机器学习中，对于处理的各种类型的数据，通常采用一些特征向量来表示。简单地将一张猫图表示为一个特征向量，可以直接把三个矩阵进行拆分重塑，最终形成维数$n_x = 64 \times 64 \times 3 = 12288 $的一个向量$x$:

特征向量

其次，实现这个分类器，需要准备大量的猫图及少量的非猫图，并取其中大部分组成该分类器的训练样本，少部分组成测试样本。将这些样本都以上述的方式表示为特征向量的形式，一个样本由一对$(x,y)$进行表示，其中x为$n_x$维的特征向量，$y$是该特征向量的标签（Label），根据该特征向量表示的是猫或非猫，取值为$0$或$1$。如果有$m$个训练样本对，它们将被表示为：$$ {(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})} $$

更进一步，可以用矩阵的形式将我们的数据表示得更为紧凑。训练集中所有特征向量$x^{(1)}$、$x^{(2)}$…以及它们的标签$y^{(1)}$、$y^{(2)}$…分别进行列组合，变成两个矩阵$X$、$Y$：$$ {X = [x^{(1)},x^{(2)},…,x^{(m)}]}$$ $$ {Y = [y^{(1)},y^{(2)},…,y^{(m)}]}$$
这样，$X$会是个大小为$n_x \times m$的矩阵，$Y$是个大小为$1 \times m$的矩阵。

Logistic回归模型

Logistic回归是一种用于解决监督学习（Supervised Learning）问题的学习算法。进行Logistic回归的目的，是使训练数据的标签值与预测出来的值之间的误差最小化。建立猫图分类器的Logistic回归模型过程如下：

猫图分类器中，要实现的是：对于给定的以$n_x$维特征向量$x$表示、标签为$y$的一张图片，估计出这张图片为猫图的概率$\hat{y}$，即：$$\hat{y} = p(y = 1|x), 0 \le \hat{y} \le 1$$

有大量猫图的数据时，考虑采用线性拟合的方法，来找到一个$\hat{y}$关于$x$的函数，从而实现这个猫分类器。规定一个$n_x$维向量$w$和一个值$b$作为参数，可得到线性回归的表达式：$${\hat{y} = w^Tx + b}$$

由于$\hat{y}$为概率值，取值范围为$[0,1]$，简单地进行线性拟合，得出的$\hat{y}$可能非常大，还可能为负值。此时，就需要用一个Logistic回归单元来对其值域进行约束。这里以sigmoid函数为逻辑回归单元，其表达式为：$$\sigma{(z)} = \frac{1}{1+e^{-z}}$$

函数图像为：

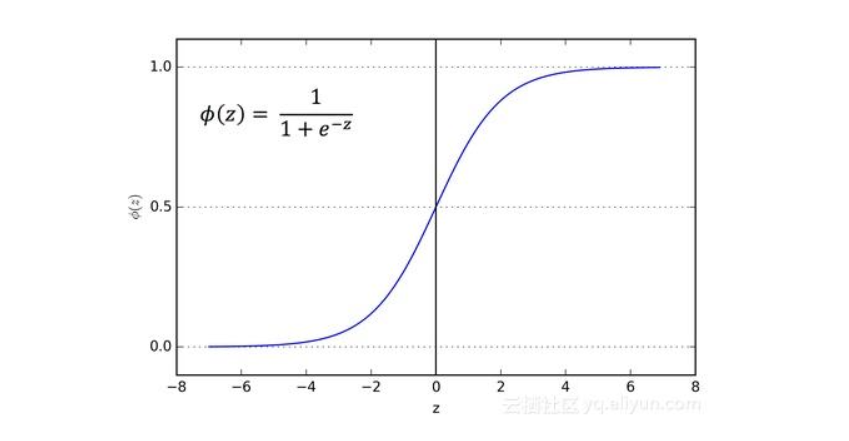
sigmoid函数

从中可以看出，sigmoid函数具有如下性质：

  • 当$z$趋近于正无穷大时，$\sigma{(z)} = 1$;
  • 当$z$趋近于负无穷大时，$\sigma{(z)} = 0$;
  • 当$z = 0$时，$\sigma{(z)} = 0.5$。

所以可以用sigmoid函数来约束$\hat{y}$的值域，得到该分类器的Logistic回归模型：$${ \hat{y} = σ(w^Tx + b) = \frac{1}{1+e^{-(w^Tx + b)}}}$$

建立好Logistic回归模型后，接下来要考虑的是如何利用我们的训练集数据，找到该模型中的两个参数$w$和$b$的最优解。

成本函数

为了训练逻辑回归模型中的参数w和b，使得输出值$\hat{y}$与真实值y尽可能一致，即尽可能准确地判断一张图是否为猫，需要定义一个成本函数（Cost Function）作为衡量的标准。

单个样本的预测值（${\hat y}^{(i)}$）与其真实值（$y^{(i)}$）之间的误差大小用损失函数（Loss Function）来衡量。平方误差（Square Loss）就是一种常用的损失函数，其表达式为：$${\mathcal{L}(\hat y,y)=\frac{1}{2}(\hat y-y)^2}$$

但Logistic回归中，一般不采用这个损失函数，因为在训练参数过程中，使用这个损失函数将得到一个非凸函数而存在很多个局部最优解，使得后面可能无法使用梯度下降（Gradient Descent）来得到我们想要的最优解。

对这个Logistic回归模型，希望能够满足如下条件概率：
$$p(y|x) = \begin{cases} \hat{y}, & \text{$(y=1)$} \\ 1 - \hat{y}, & \text{$(y=0)$} \end{cases}$$

将上下两个式子合二为一，可写成：$$p(y|x) = \hat{y}^y (1 - \hat{y})^{(1 - y)} $$

对两边取对数，进一步化简为：$$log\ p(y|x) = ylog\ \hat y+(1-y)log\ (1-\hat y) $$

我们希望$p(y|x)$的值越大越好，而损失越小越好。所以为上式添上负号，就可以将它作为一个损失函数，这便是应用很广的交叉熵（Cross Entropy）损失函数，表达式为：$${\mathcal{L}(\hat y,y)=-[ylog\ \hat y+(1-y)log\ (1-\hat y)]}$$

交叉熵损失函数有如下性质：

  • 当$y^{(i)}=1$时，${\mathcal{L}({\hat y}^{(i)},y^{(i)})=-log\ {\hat y}^{(i)}}$，意味着损失越小，$\hat{y}$越接近于1；
  • 当$y^{(i)}=0$时，${\mathcal{L}({\hat y}^{(i)},y^{(i)})=-log\ (1-{\hat y}^{(i)})}$，意味着损失越小，$\hat{y}$越接近0。

对m个训练样本整体的成本函数，可以使用数理统计中的参数估计方法之一–最大似然估计法（Maximum Likelihood Estimation）推导出来的。

假设所有训练样本独立同分布，则它们的联合概率为所有样本概率的乘积，得到似然函数为:
$$P (x) = \prod_{i=1}^m p(y^{(i)}|x^{(i)})$$

两边取对数有：
$$log\ P(x) = \sum_{i=1}^m log\ p(y^{(i)}|x^{(i)}) = - \sum_{i=1}^m \mathcal{L}(\hat{y}^{(i)}, y^{(i)})$$

最大似然估计中的下一步，是求解出一组使得上式取得最大值的 参数。而在这里，由于我们训练模型时，目标是使成本函数最小化，所以不直接使用上式作为成本函数，而将其负号去掉，同时为方便处理数据，而乘上一个常数$1/m$对式子适当进行放缩，最后得到下面的成本函数：
$${J(w,b) = \frac{1}{m} \sum_{i=1}^m \mathcal{L}({\hat y}^{(i)}, y^{(i)}) = - \frac{1}{m} \sum_{i=1}^m [ylog\ \hat y+(1-y)log\ (1-\hat y)]}$$

梯度下降

要找到参数的最优解，一般采用梯度下降法。

标量场中某一函数上某一点的梯度，指向该函数在该点处增长最快的方向，函数在该点处沿着该方向变化最快且变化率最大。

在空间坐标中以$w$，$b$为轴，画出的损失函数$J$的图像将类似于下图，要找到函数取得最小值的最优参数，先为$w$和$b$赋一个初始值，正如下图的最上面的红点。

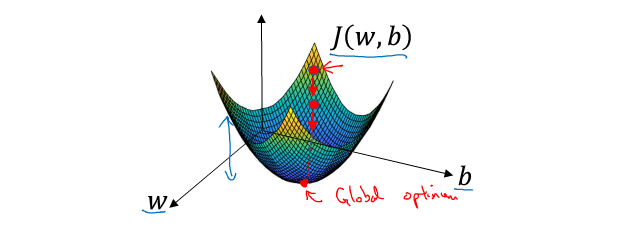
J(w,b)图像

对Logistic回归模型，因为成本函数是凸函数，无论参数的初始值是多少，最后总能到达同一个点或大致相同的点，所以几乎任何初始化方法都有效，于是通常将参数直接初始化为0。

所谓的梯度下降，就是从起始点开始，试图每次都沿最陡峭的下降方向下坡，尽可能快地到达最低点即凸函数取得最小值的点，而下坡的方向便是各点上的梯度值。

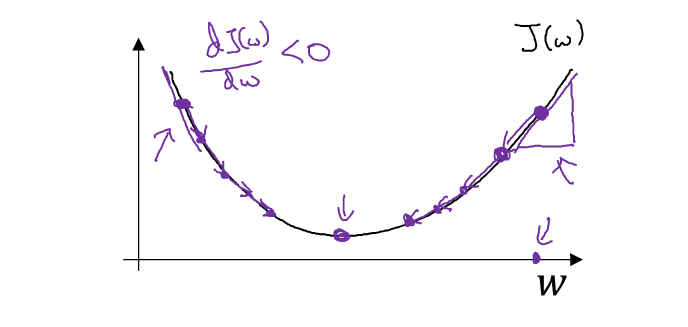
J(w,b)二维图像

从一个二维上的图像看，函数的导数方向即为梯度方向，下降速度最快。即每经过一次梯度下降，参数$w$、$b$即更新为：$${w = w-\alpha\frac{\partial J(w,b)}{\partial w}}$$
$${b = b-\alpha\frac{\partial J(w,b)}{\partial b}}$$

式中的$\alpha$被称为学习率，通常为一个小于1的值，用于控制梯度下降过程中每一次移动的规格大小，好比于下降时每一次迈步的大小。$\alpha$的不宜太小也不宜过大：太小会使迭代次数增加，容易陷入局部最优解；太大容易错过最优解。

由梯度下降法，由训练数据经过多次迭代，就可以求得使成本函数的取得最小值的参数$w$和$b$，从而建立好Logistic模型，实现我们想要的猫图分类器。

Python实现

使用Python编写一个逻辑回归分类器来识别猫，以此来了解如何使用神经网络的思维方式来进行这项任务，识别过程如图：

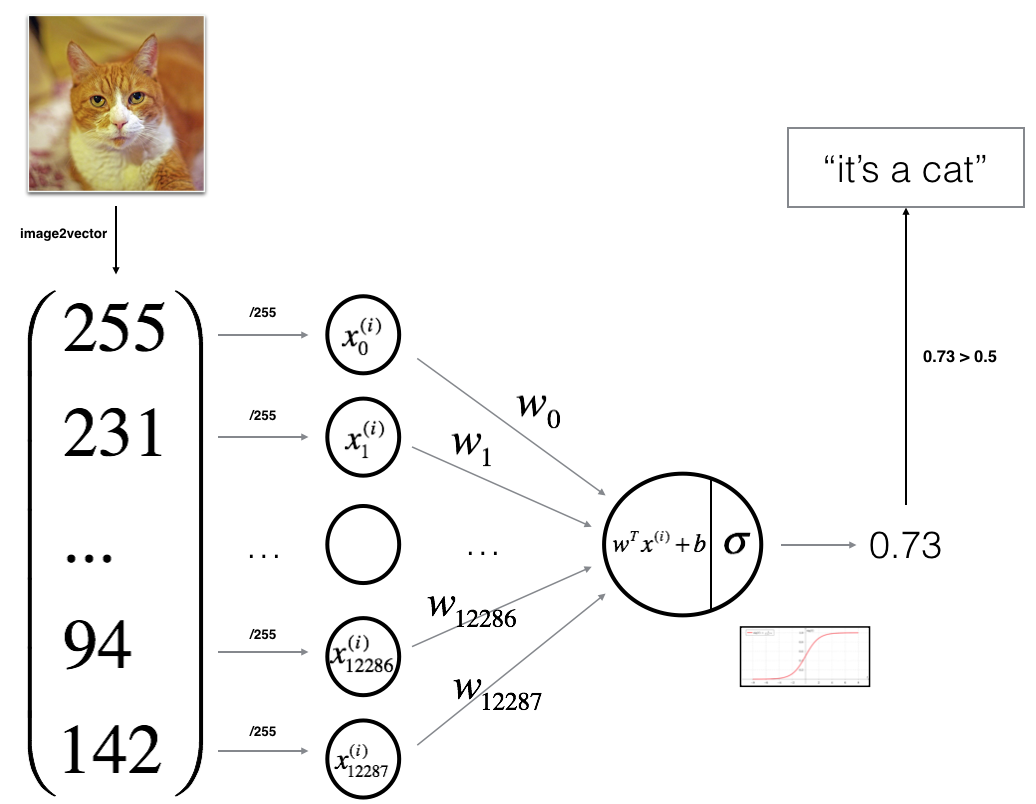
识别过程示意图

实现过程

其中用到的Python包有：

  • numpy是使用Python进行科学计算的基础包。
  • matplotlib是Python中著名的绘图库。
  • h5py在Python提供读取HDF5二进制数据格式文件的接口，本次的训练及测试图片集是以HDF5储存的。
  • PIL(Python Image Library)为Python提供图像处理功能。
  • scipy基于NumPy来做高等数学、信号处理、优化、统计和许多其它科学任务的拓展库。
    几个Python包的安装及基本使用方法详见官网。

1.导入要用到的所有包

1
2
3
4
5
6
7
#导入用到的包
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage

2.导入数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#导入数据
def load_dataset():
    train_dataset = h5py.File("train_cat.h5","r") #读取训练数据，共209张图片
    test_dataset = h5py.File("test_cat.h5", "r") #读取测试数据，共50张图片

    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) #原始训练集（209*64*64*3）
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) #原始训练集的标签集（y=0非猫,y=1是猫）（209*1）

    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) #原始测试集（50*64*64*3
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) #原始测试集的标签集（y=0非猫,y=1是猫）（50*1）

    train_set_y_orig = train_set_y_orig.reshape((1,train_set_y_orig.shape[0])) #原始训练集的标签集设为（1*209）
    test_set_y_orig = test_set_y_orig.reshape((1,test_set_y_orig.shape[0])) #原始测试集的标签集设为（1*50）

    classes = np.array(test_dataset["list_classes"][:])
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

需要说明的是，本次的训练及测试图片集是以HDF5格式储存的,train_cat.h5、test_cat.h5文件打开后结构如下：

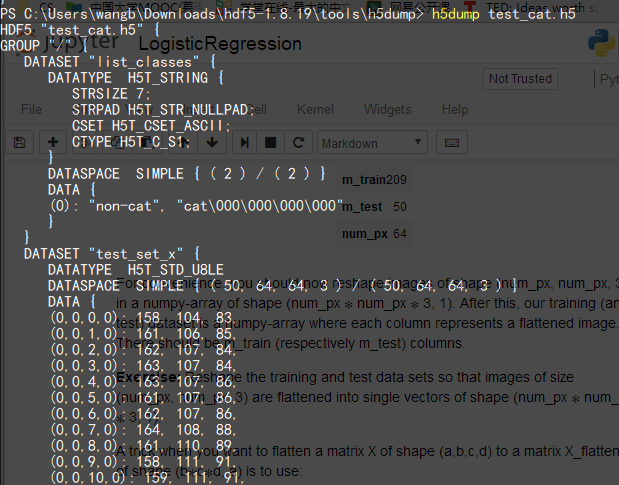
h5文件结构

另外，也可以调用以下方法来查看训练集或测试集中的图片：

1
2
3
4
5
6
7
8
9
#显示图片
def image_show(index,dataset):
    index = index
    if dataset == "train":
        plt.imshow(train_set_x_orig[index])
        print ("y = " + str(train_set_y[:, index]) + ", 它是一张" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") +  "' 图片。")
    elif dataset == "test":
        plt.imshow(test_set_x_orig[index])
        print ("y = " + str(test_set_y[:, index]) + ", 它是一张" + classes[np.squeeze(test_set_y[:, index])].decode("utf-8") +  "' 图片。")

3.sigmoid函数

1
2
3
4
#sigmoid函数
def sigmoid(z):
    s = 1/(1+np.exp(-z))
    return s

4.初始化参数w，b

1
2
3
4
5
#初始化参数w,b
def initialize_with_zeros(dim):
    w = np.zeros((dim,1)) #w为一个dim*1矩阵
    b = 0    
    return w, b

5.计算Y_hat,成本函数J以及dw，db

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#计算Y_hat,成本函数J以及dw，db
def propagate(w, b, X, Y):
    m = X.shape[1] #样本个数
    Y_hat = sigmoid(np.dot(w.T,X)+b)                                     
    cost = -(np.sum(np.dot(Y,np.log(Y_hat).T)+np.dot((1-Y),np.log(1-Y_hat).T)))/m #成本函数

    dw = (np.dot(X,(Y_hat-Y).T))/m
    db = (np.sum(Y_hat-Y))/m

    cost = np.squeeze(cost) #压缩维度    
    grads = {"dw": dw,
             "db": db} #梯度

    return grads, cost

6.梯度下降找出最优解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#梯度下降找出最优解
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):#num_iterations-梯度下降次数 learning_rate-学习率，即参数ɑ
    costs = [] #记录成本值

    for i in range(num_iterations): #循环进行梯度下降
        grads, cost = propagate(w,b,X,Y)
        dw = grads["dw"]
        db = grads["db"]

        w = w - learning_rate*dw
        b = b - learning_rate*db

        if i % 100 == 0: #每100次记录一次成本值
            costs.append(cost)

        if print_cost and i % 100 == 0: #打印成本值
            print ("循环%i次后的成本值: %f" %(i, cost))

    params = {"w": w,
              "b": b} #最终参数值

    grads = {"dw": dw,
             "db": db}#最终梯度值

    return params, grads, costs

7.得出预测结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#预测出结果
def predict(w, b, X):
    m = X.shape[1] #样本个数
    Y_prediction = np.zeros((1,m)) #初始化预测输出
    w = w.reshape(X.shape[0], 1) #转置参数向量w

    Y_hat = sigmoid(np.dot(w.T,X)+b) #最终得到的参数代入方程

    for i in range(Y_hat.shape[1]):
        if Y_hat[:,i]>0.5:
            Y_prediction[:,i] = 1
        else:
            Y_prediction[:,i] = 0

    return Y_prediction

8.建立整个预测模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#建立整个预测模型
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False): #num_iterations-梯度下降次数 learning_rate-学习率，即参数ɑ
    w, b = initialize_with_zeros(X_train.shape[0]) #初始化参数w，b

    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost) #梯度下降找到最优参数

    w = parameters["w"]
    b = parameters["b"]

    Y_prediction_train = predict(w, b, X_train) #训练集的预测结果
    Y_prediction_test = predict(w, b, X_test) #测试集的预测结果

    train_accuracy = 100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100 #训练集识别准确度
    test_accuracy = 100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100 #测试集识别准确度

    print("训练集识别准确度: {} %".format(train_accuracy))
    print("测试集识别准确度: {} %".format(test_accuracy))

    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test,
         "Y_prediction_train" : Y_prediction_train,
         "w" : w,
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}

    return d

9.初始化样本，输入模型，得出结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#初始化数据
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()

m_train = train_set_x_orig.shape[0] #训练集中样本个数
m_test = test_set_x_orig.shape[0] #测试集总样本个数
num_px = test_set_x_orig.shape[1] #图片的像素大小

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T #原始训练集的设为（12288*209）
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T #原始测试集设为（12288*50）

train_set_x = train_set_x_flatten/255. #将训练集矩阵标准化
test_set_x = test_set_x_flatten/255. #将测试集矩阵标准化

d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

结果分析

运行程序最终得到的结果为：

结果

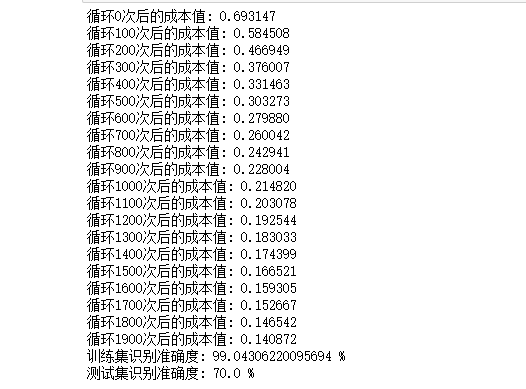
训练集识别准确率接近100％，测试集的准确率有70％。由于训练使用的小数据集，而且逻辑回归是线性分类器，所以这个结果对于这个简单的模型实际上还是不错。

使用mathplotlib画出学习曲线：

1
2
3
4
5
6
7
# 画出学习曲线
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

学习曲线

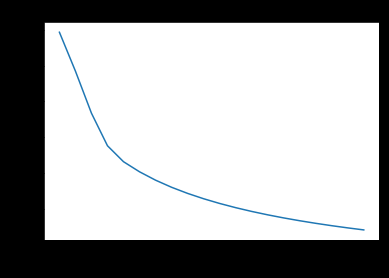
学习率不同时的学习曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
    print ("学习率: " + str(i))
    models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
    print ('\n' + "-------------------------------------------------------" + '\n')

for i in learning_rates:
    plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()

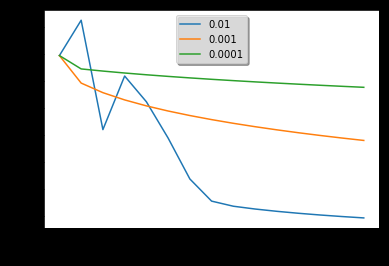
几个不同学习率下的学习曲线

说明不同的学习率会带来不同的成本，从而产生不同的预测结果。

参考资料

  1. 吴恩达-神经网络与深度学习-网易云课堂
  2. Andrew Ng-Neural Networks and Deep Learning-Coursera
  3. 课程代码与资料-GitHub

注：本文涉及的图片及资料均整理翻译自Andrew Ng的Deep Learning系列课程，版权归其所有。翻译整理水平有限，如有不妥的地方欢迎指出。

更新历史：

  • 2017.09.13 完成初稿
  • 2017.09.17 修正部分错误
  • 2018.02.13 修改部分内容
  • 2019.01.10 修改部分内容

深度学习(1)：Logistic回归

https://hugsy.top/2017/09/12/ML/deep_learning_1/

作者

Hugsy

发布于

2017-09-12

更新于

2022-12-10

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

×